Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение

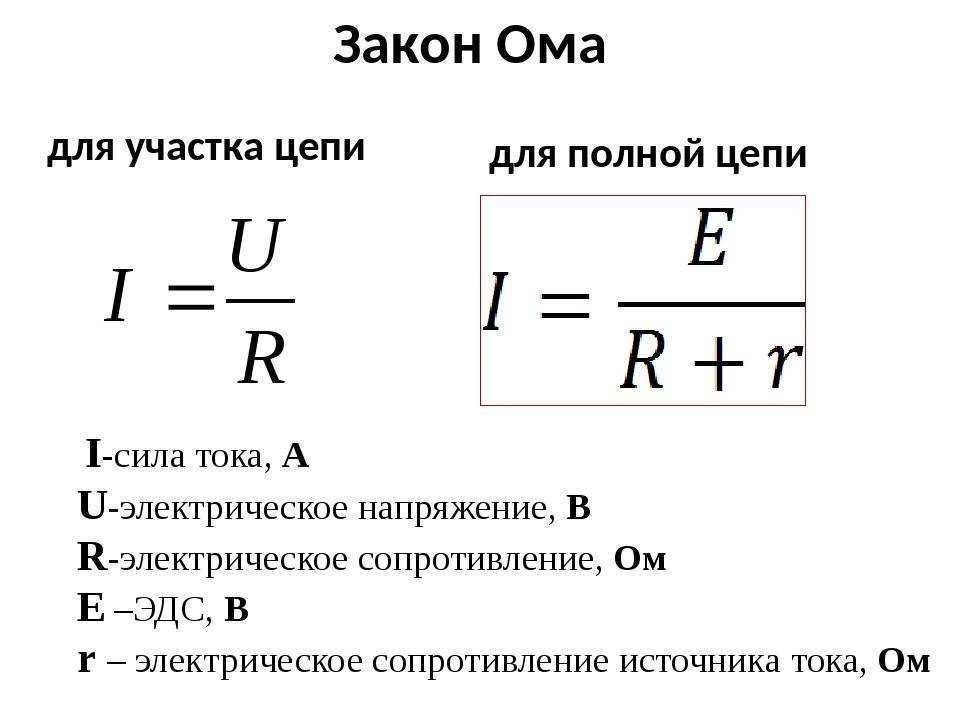
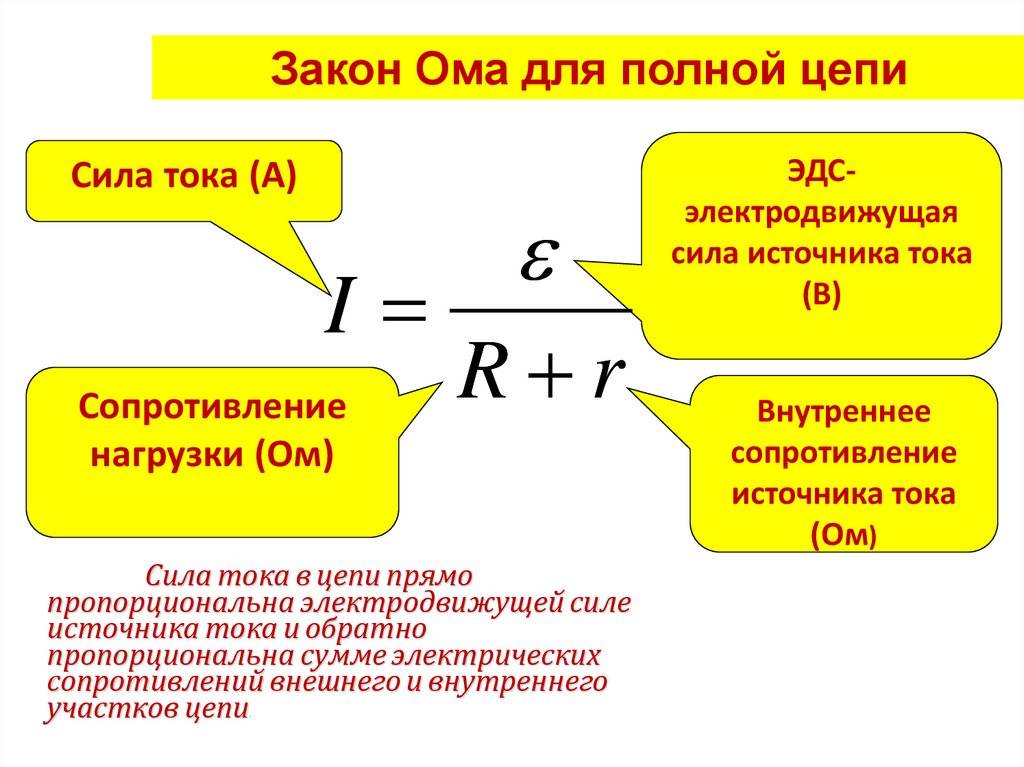
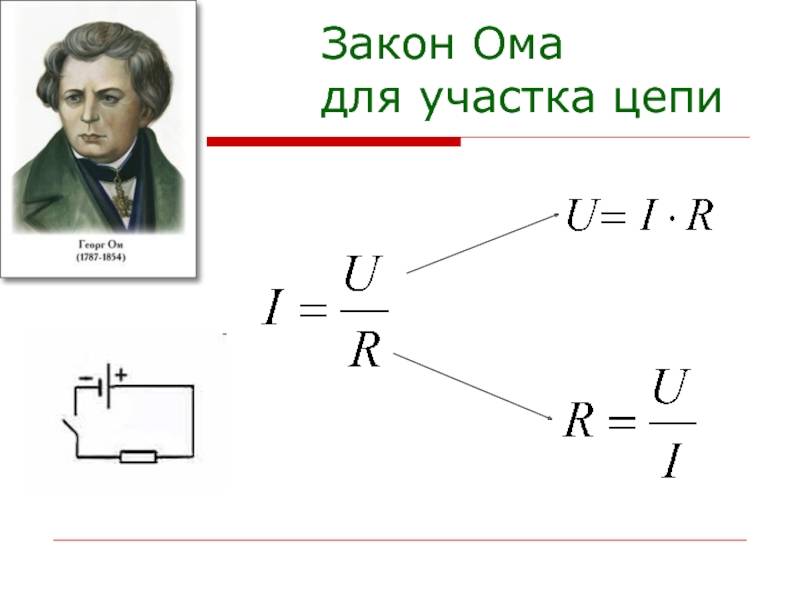
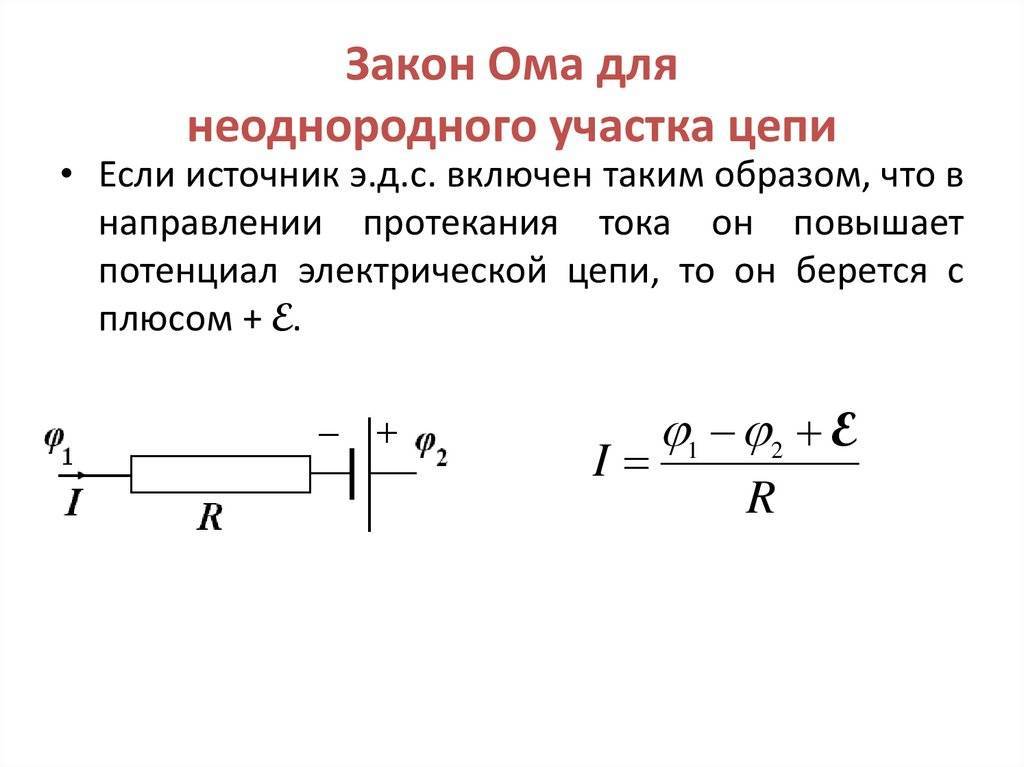
Закон ома в интегральной форме

Закон Ома (в интегральной форме).

	j2 > j1	закон Ома для однородного участка цепи (без источника тока); смысл закона в том, что сила тока прямо пропорциональна разности потенциалов, приложенной к концам проводника
(·)		закон Ома для неоднородного участка цепи (с источником тока) (о выборе знаков см. дальше)
	закон Ома для замкнутой цепи Во внешней цепи традиционно считается, что ток идет от «+» батареи к «-»
В формулах: R – суммарное сопротивление участка цепи, указанного символически прямоугольником; оно может состоять из нескольких проводников, соединенных и последовательно, и параллельно — общая ЭДС источников тока — это может быть несколько батарей, соединенных параллельно или последовательно; r – общее внутреннее сопротивление источников тока

Напряжением U называется произведение силы тока на сопротивление участка. Из формулы (·) следует, что напряжение и разность потенциалов численно равны только для однородного участка цепи ( = 0).

Перепишем (·), выразив разность потенциалов, т. к. вольтметр измеряет именно разность потенциалов, а не напряжение (они равны только для однородного участка): . Пусть требуется найти разность потенциалов Dj = j2 — j1. Выбрать знаки можно с помощью такого ненаучного правила: «Идем» по цепи от j2 к j1, если ток – с нами – берем «+», если упираемся в «+» батареи, — берем «+». Если при числовых расчетах получим, например, (-5 В) это означает, что j2 j1.

1. Вывод закона Ома на основе электронной теории электропроводности металлов.
2. В электронной теории проводимости предполагается:
3. 1) В металлах имеются свободные электроны, которые в отсутствие внешнего
4. электрического поля движутся хаотически, а при
5. наличии поля приобретают характер упорядоченного

движения (см. рис.).

• 2) Движение каждого электрона подчиняется законам
• классической механики.
• 3) Все вместе электроны образуют электронный газ и подчиняются законам
• молекулярной физики.
• 4) Взаимодействие электронов с ионами решетки рассматривается как простое
• столкновение, взаимодействием электронов между собой пренебрегается.
• 5) Напряженность поля внутри металла считается постоянной.
• 6) Все электроны под действием внешнего электрического поля приобретают
• одинаковые скорости vср.

При выводе закона Ома будем считать, что электрон, сталкиваясь с ионом, полностью отдает ему свою энергию, а затем снова набирает скорость под действием сил поля (см. рис.- фрагмент кристаллической решетки).

Электрон в кристалле участвует одновременно в двух движениях: хаотическом тепловом со скоростью u @ 105 м/с и направленном под действием поля со скоростью vср порядка 0,001 м/с, т. е.

u >> vср

II закон Ньютона для электрона
из кинематики, t – время движения электрона между двумя столкновениями
средняя скорость электрона за время между двумя столкновениями
l — средняя длина свободного пробега электрона – это расстояние, которое проходит электрон между двумя последовательными столкновениями с ионами (u >> vср)
(··)	плотность тока в проводнике; подставив в эту формулу вышеприведенные, получим:
мы получили закон Ома в дифференциальной форме, запишем его в векторном виде:

закон Ома в дифференциальной форме. В такой форме закон применим для бесконечно малого объема проводника, фактически – для точки проводника.
(···)	s — удельная электропроводность проводника;r — удельное сопротивление проводника

Электронная теория проводимости металлов, несмотря на множество упрощающих предположений, позволяет теоретически вывести закон Ома и закон Джоуля – Ленца (см. ниже). Это свидетельствует о том, что модель поведения электронов в металле соответствует действительности. Вместе с тем эта теория столкнулась с рядом трудностей. Рассмотрим некоторые из них.

1)Теплоемкость металла теоретически должно складываться из теплоемкости кристаллической решетки и теплоемкости электронов: СМе = Среш +Сэлнов=

6R/2 + 3R/2 (для моля). Но из опыта следует, что теплоемкость почти всех твердых тел равна 3R. Таким образом, получается, что электроны не участвуют в теплоемкости, т. е.

III часть курса).

2)В формуле (···) e,m известны, n, u – можно вычислить, а s = 1/r измерить опытным путем. Таким образом можно оценить длину свободного пробега электрона l. Она оказалась равной порядка 10-5 см, тогда как расстояние между ионами примерно 10-8 см.

Получается, что электрон пролетает мимо сотен ионов, не сталкиваясь с ними. Это затруднение также объяснила квантовая механика: движение электрона в металле – это распространение некоторой волны, искажение этой волны происходит на примесях (чужеродных атомах), а их металле значительно меньше, чем атомов решетки.

Практическое использование

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.

Применяем закон к любому участку цепи.

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.

Находим силу тока

Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

• R=0,2 МОм;
• U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА). Вычисление напряжения Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

• R=20 кОм;
• I=10 мА.

Преобразуем исходные данные:

• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим. Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

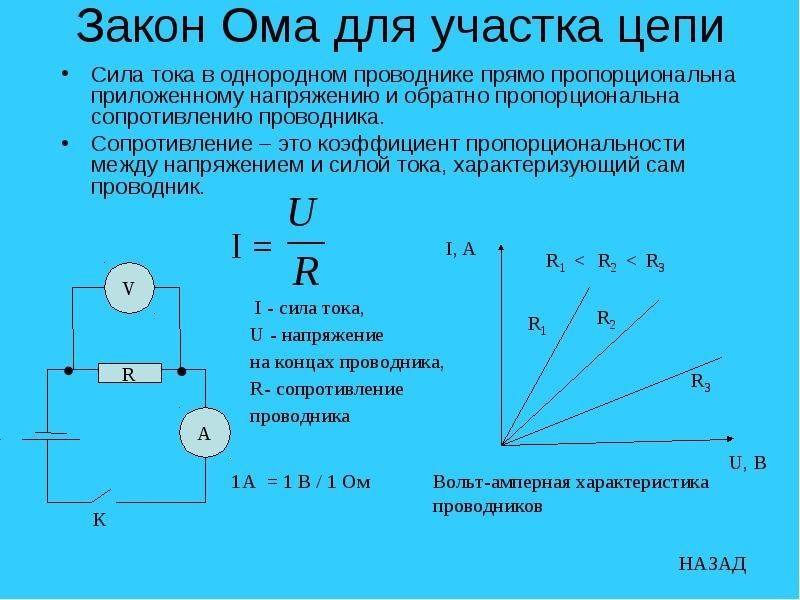
Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении

Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Последовательное и параллельное включение элементов

Элементы полной цепи или участка цепи могут соединяться последовательно или параллельно. Для каждого варианта действие тока и напряжения будет разным, поэтому закон Ома для замкнутой цепи в обоих случаях тоже отличается. Данный физические свойства комбинированно используются в различных электрических схемах.

Цепь последовательно включенных резистивных элементов

Если в качестве примера взять два элемента на отдельном участке, то поведение основных величин можно записать в следующем виде:

• I = I1= I2 (силы токов равны)
• U = U1+ U2 (общее напряжение состоит из суммы напряжений)
• R = R1+ R2 (общее сопротивление также является суммой двух сопротивлений)

Отсюда можно сделать вывод, что вне зависимости от количества резистивных элементов 1, 2 или 3, соединенных последовательно, сила тока на участке остается неизменной. Общее значение напряжения эквивалентно источнику ЭДС, а для каждого компонента определяется основной формулой закона Ома.

Цепь параллельно включенных резистивных элементов

При параллельном подключении действие закона Ома происходит несколько иначе:

• I = I1+ I2 …  (силы токов, проходящих через элементы, складываются)
• U = U1= U2 … (все напряжения равны между собой)
• 1 / R = 1 / R1+ 1 / R2 + … (сопротивление суммируется по отдельной схеме)

Довольно часто используются смешанные схемы подключения, в которых используются оба варианта, объединенные в замкнутый контур. В этом случае сначала рассчитывается общий резистивный номинал на участке с параллельным подключением, после чего к полученному результату добавляется значение резистора на последовательном соединении.

Интегральная и дифференциальная формы закона

Все варианты, рассмотренные выше, подходят ближе к идеальным условиям, где каждый элемент имеет свой постоянный показатель. В том числе и в проводниках рассматривается однородная структура, хотя на практике такое встречается очень редко. Большинство схем состоят из множества участков, на которых используются разные проводники, отличающиеся материалом и сечением.

Интегральная форма расчетов практически совпадает с действием закона Ома для полной цепи и других его производных. Следовательно, сила тока, протекающего в проводнике, будет зависеть от разности потенциалов на его концах и его полного сопротивления. То есть, напряжение можно определить: I * R = φ1 – φ2 + έ или же U=I x R.

Дифференциальная форма используется в основном для изучения и теоретических расчетов бесконечно малых проводников на ничтожно малом участке цепи. Коротко это можно написать в таком виде:

ej = aE

В этом выражении А является удельной теплопроводностью, E – напряженностью электрического поля, j – плотностью потока частиц с электрическим зарядом. Следовательно, произведение ej будет плотностью электрического тока. Поскольку Закон Ома в данном случае касается лишь одной точки, поэтому он и получил название дифференциальной формы.

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

J=n⋅e2⋅τm⋅E=σ⋅E.{\displaystyle \mathbf {J} ={\frac {n\cdot e_{0}^{2}\cdot \tau }{m}}\cdot \mathbf {E} =\sigma \cdot \mathbf {E} .}

Здесь:

• σ{\displaystyle \sigma } — электрическая удельная проводимость;
• n{\displaystyle n} — концентрация электронов;
• e{\displaystyle e_{0}} — элементарный заряд;
• τ{\displaystyle \tau } — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
• m{\displaystyle m} — эффективная масса электрона.

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.

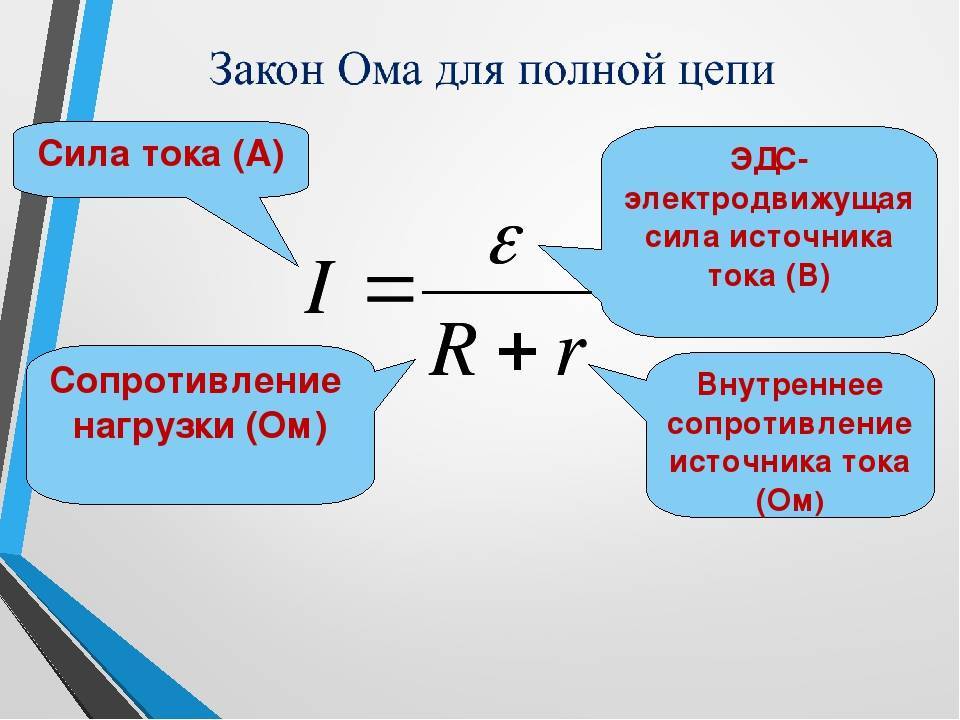
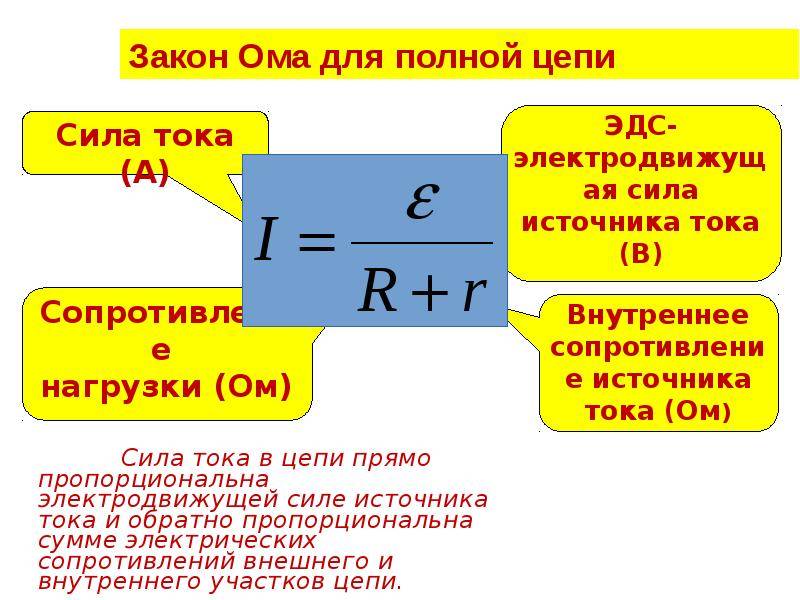
Закон Ома для полной цепи

Подробности

Просмотров: 453

«Физика – 10 класс»

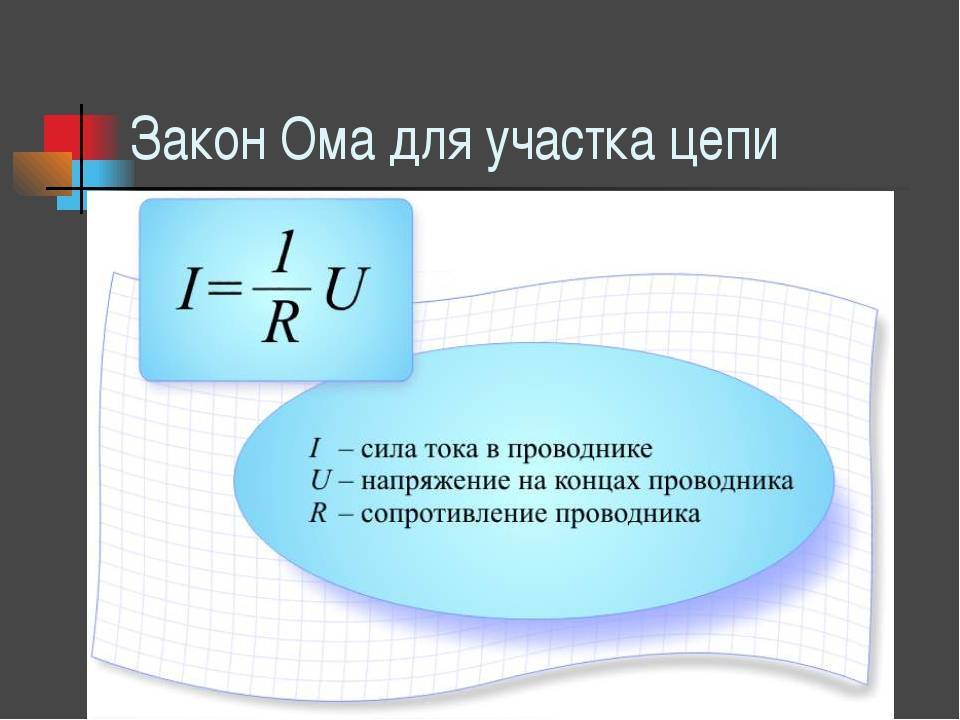
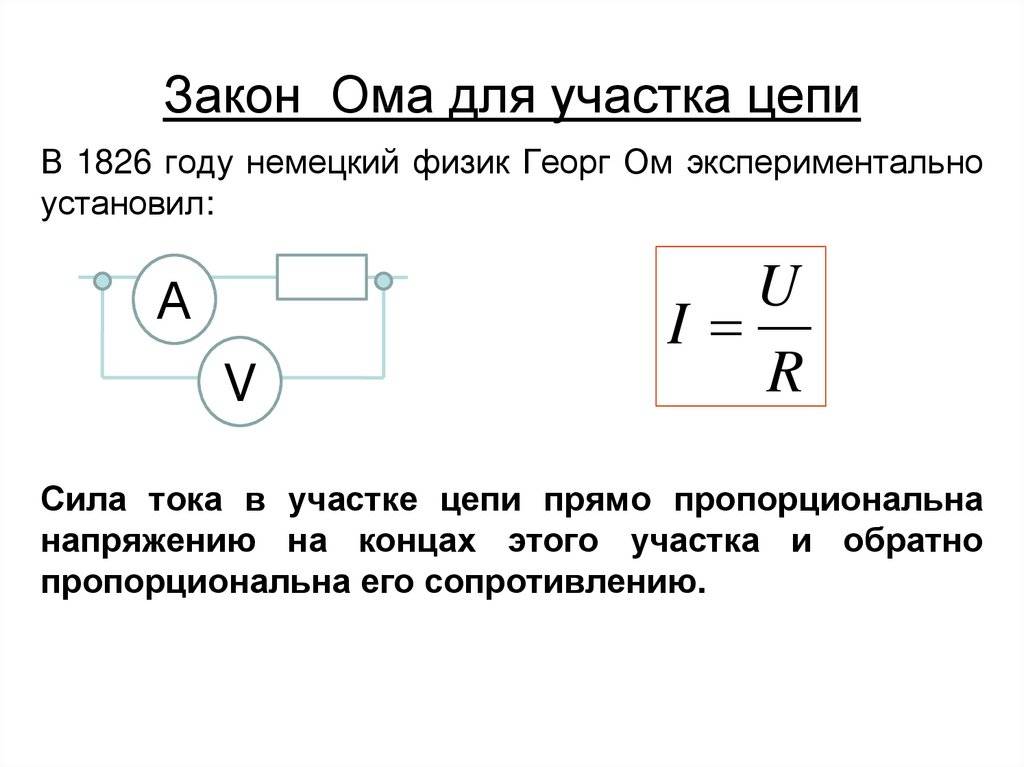
Сформулируйте закон Ома для участка цепи.
Из каких элементов состоит электрическая цепь?
Для чего служит источник тока?

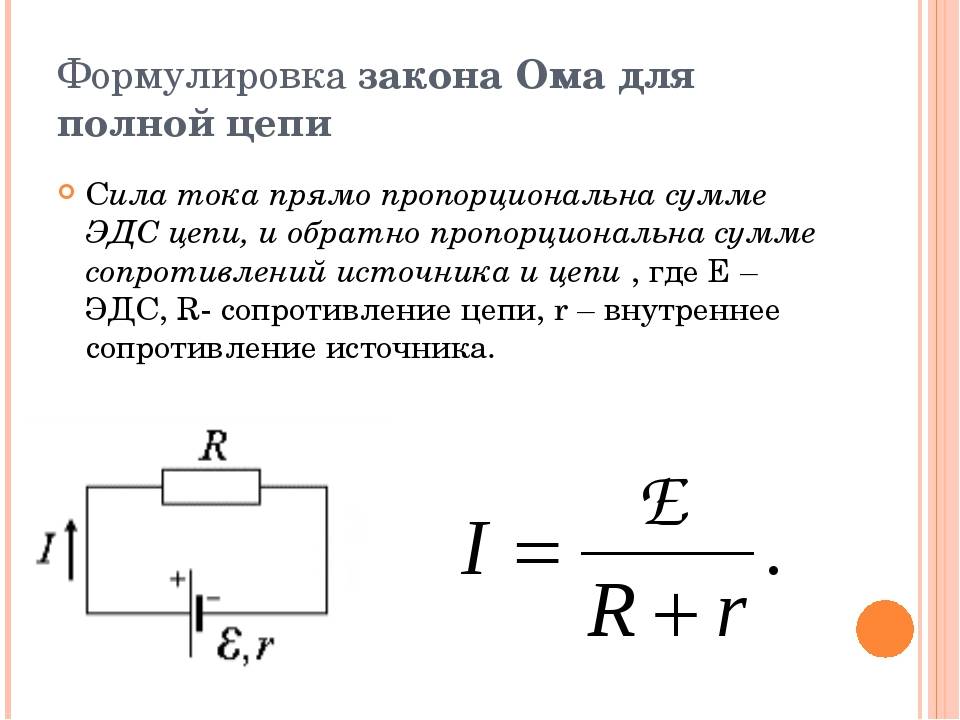
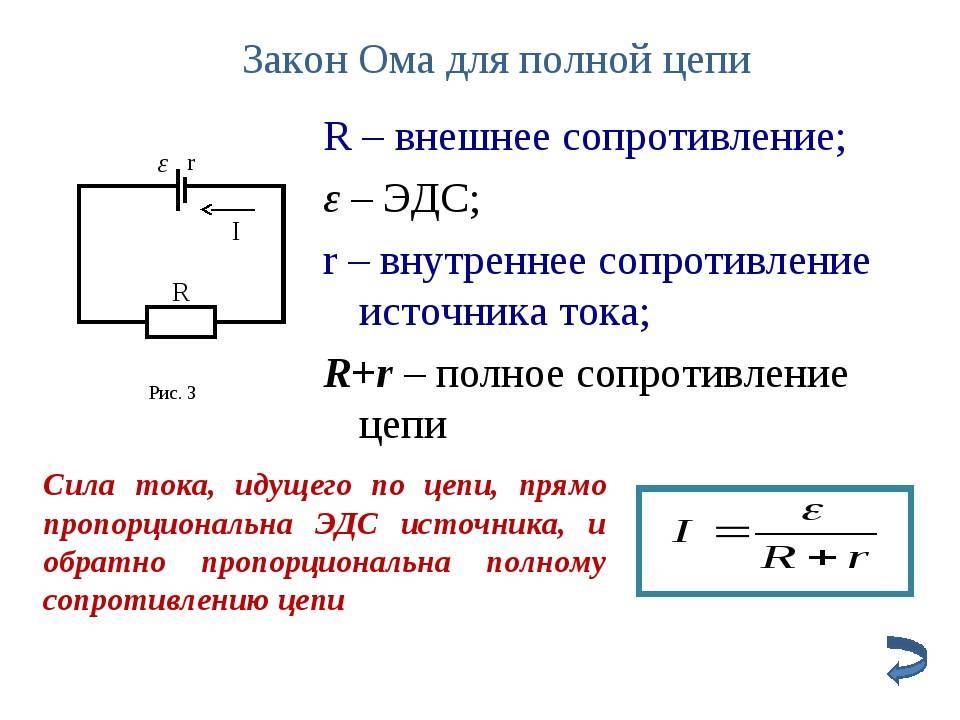
Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.

В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.

Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).

Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: А_ст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому

А_ст = ΕIΔt.         (15.17)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:

Q = I2RΔt + I2rΔt.         (15.18)

По закону сохранения энергии А_ст = Q, откуда получаем

Ε = IR + 1r.         (15.19)

Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.

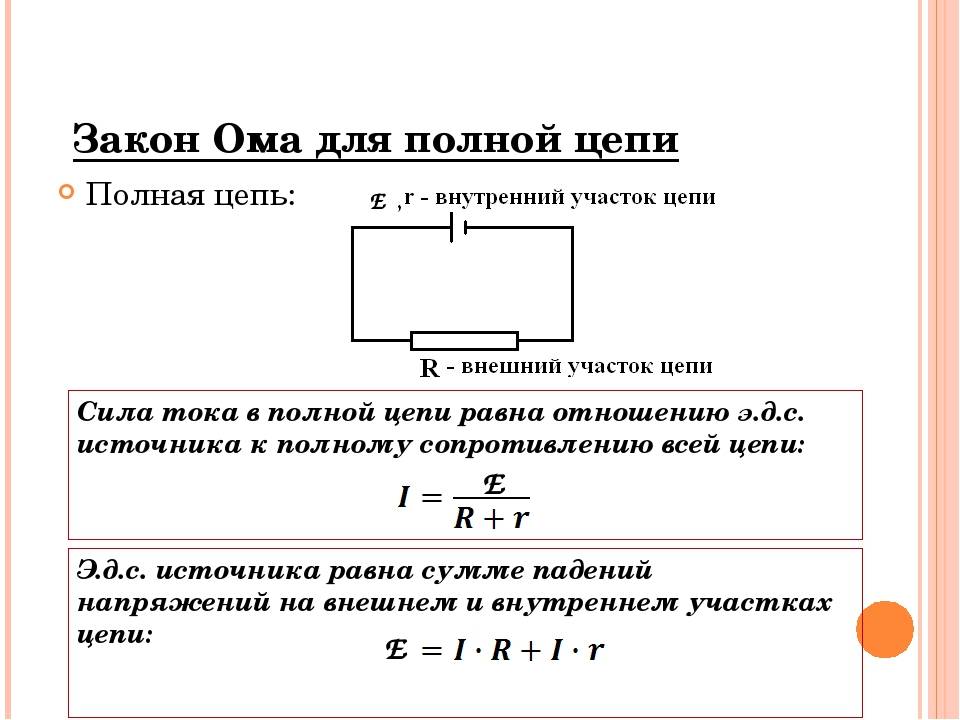
Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.

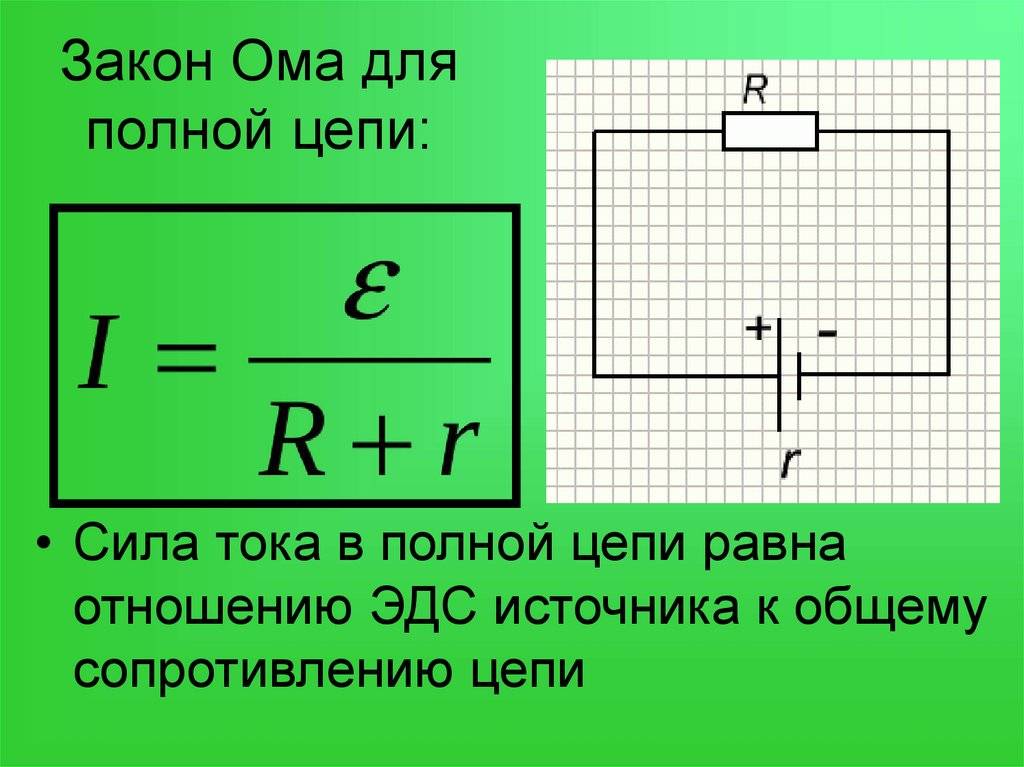
Закон Ома для замкнутой цепи:

Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.

Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε – Ir ≈ Ε

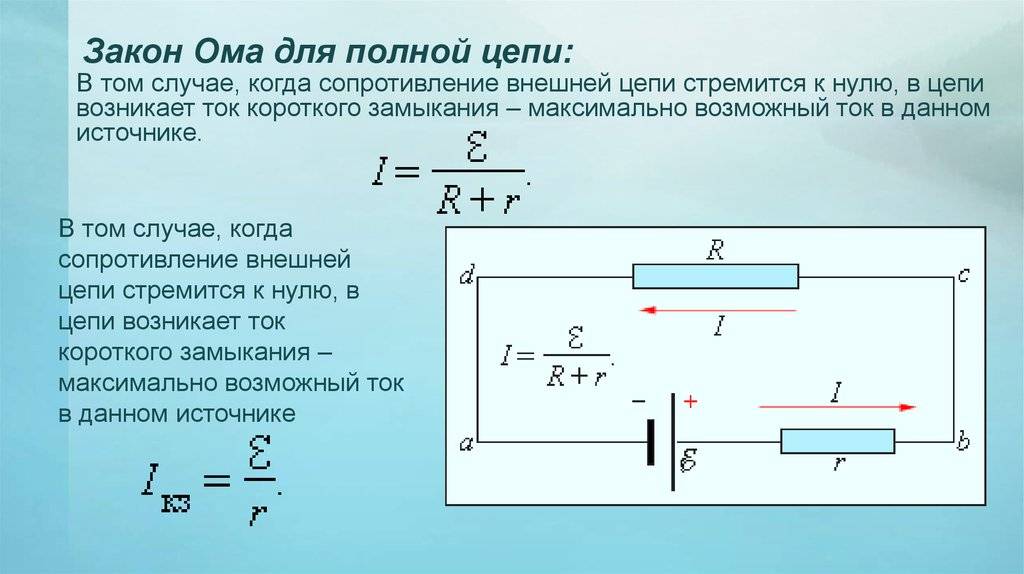
При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.

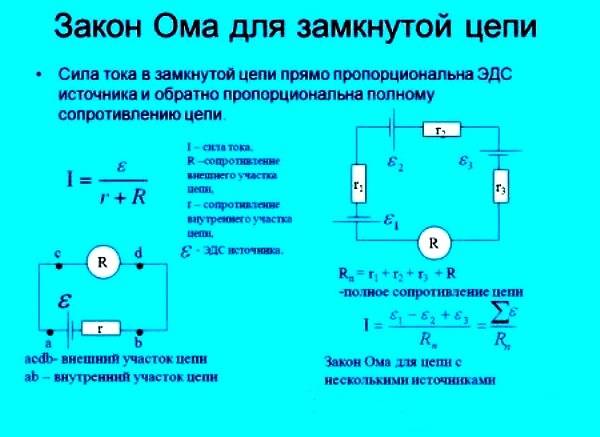
Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε₁, Ε₂, Ε₃ и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.

Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура.
На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.

Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0. Сторонние силы внутри источника совершают при этом положительную работу.

Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:

Ε_п = Ε₁ + Ε₂ + Ε₃ = lΕ₁| – |Ε₂| + |Ε₃|

Если Ε_п > 0, то согласно формуле (15.20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Ε_п < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи R_п равно сумме всех сопротивлений (см. рис. 15.11):

R_п = R + r₁ + r₂ + r₃.

Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):

I₁R₁+ I₂R₂ + … + I_nR_n = Ε₁ + Ε₂ + … + Ε_m

Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»

Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока – Физика, учебник для 10 класса – Класс!ная физика

Электрический ток. Сила тока —
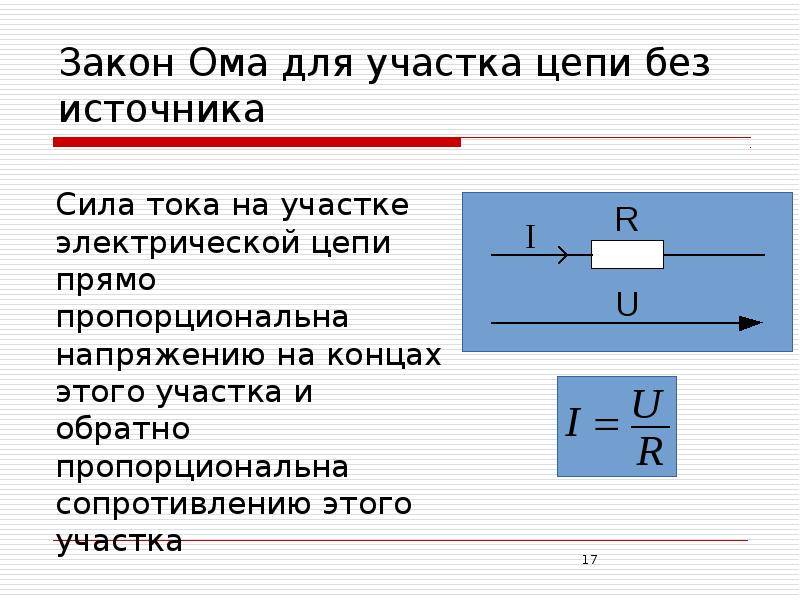
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Чему равно напряжение.

Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

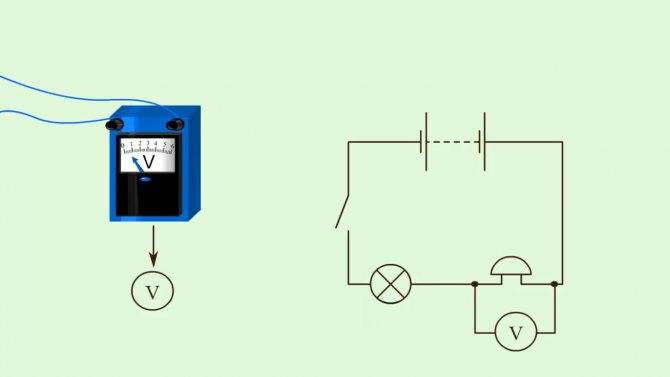Изображение вольтметра и электрической цепи

Напряжение обозначается латинской , а измеряется в . Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Вам это будет интересно Чему равен 1 ампер в киловаттах

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении. Электрическое поле. Электрическое поле

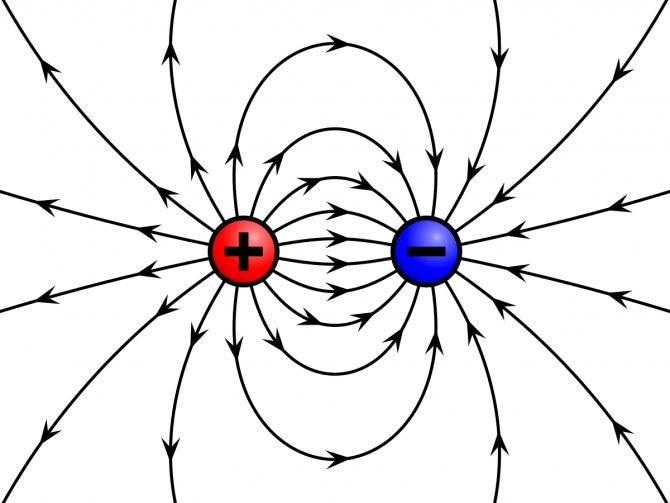Электрическое поле

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1 = I2 ;
• U = U1 + U2 ;
• R = R1 + R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1 + I2 … ;
• U = U1 = U2 … ;
• 1 / R = 1 / R1 + 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

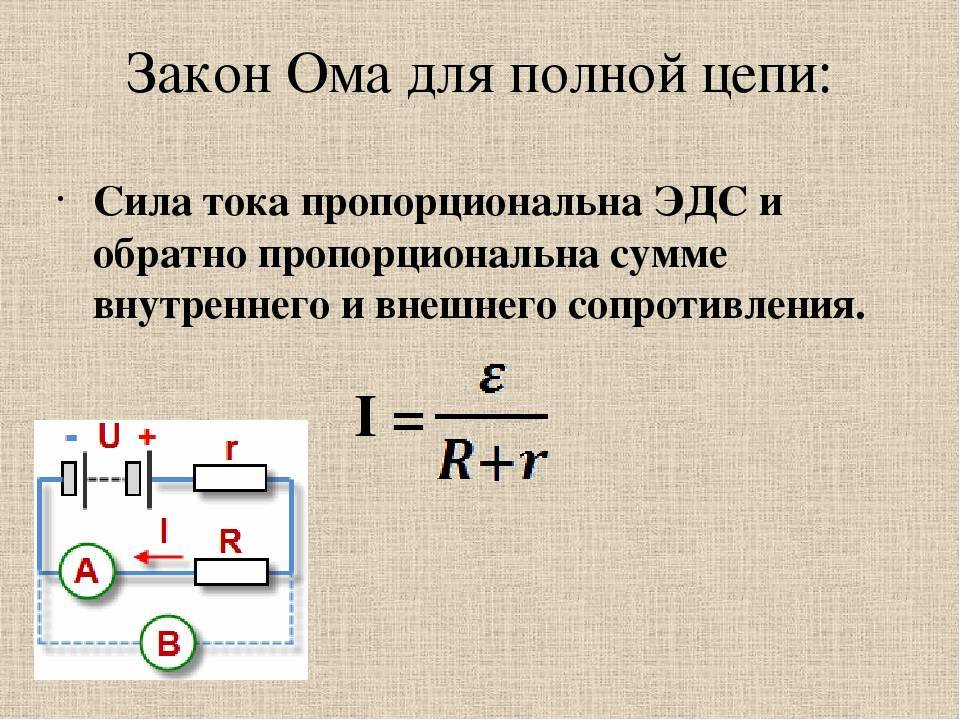
Закон Ома для полной цепи

Открытый Г

Омом закон для участка цени в общем случае справедлив и для полной цепи, если принимать во внимание как внешнюю, так и внутреннюю части цепи. Математическую запись закона Ома для этого случая можно получить на основании закона сохранения энергии, универсального для всех процессов в природе

Пусть электрическая цепь состоит из источника тока, имеющего ЭДС и внутреннее сопротивление г, и проводника сопротивлением R (рис. 1.51).

Pиc. 151. Замкнутая электрическая цепь

Согласно закону сохранения энергии работа сторонних сил равна сумме работ электрического тока во внешней и внутренней частях цепи:

По определению

Отсюда

Если учесть, что по закону Ома для участка цепи U =IR, то получим формулу этого закона для полной цепи:

Таким образом, сила тока в полной цепи пропорциональна электроднижущей силе источника и обратно пропорциональна полному сопротивлению цепи.

Сила тока в полной цепи пропорциональна электродвижущей силе источника и обратно пропорциональна полному сопротивлению цепи:

Пользуясь законом Ома для полной цепи, можно рассчитать два экстремальных случая н электрической цепи – короткое замыкание и разомкнутую цепь. Если сопротивление внешней цепи стремится к нулю (короткое замыкание), то сила тока в цепи

Это будет максимальное значение силы тока для данной цепи.
Если цепь разорвана (R→∞ ), то ток в цени прекращается при любых значениях ЭДС и внутреннего сопротивления. В последнем случае напряжение нм полюсах источника тока будет равно электродвижущей силе. Поэтому иногда дают упрощенное определение ЭДС: это величина, равная напряжению на клеммах источника при разомкнутой цепи.

Источники тока могут соединяться в батареи. Существуют несколько способов соединения источников тока.

Последовательным называют соединение, при котором соединяются друг с другом разноименные полюса источников: положительный предыдущего с отрицательным следующего и т. д. (рис. 1.52). Чаще всего соединяют источники с одинаковыми характеристиками, поэтому при последовательном соединении N источников ЭДС батареи будет в N раз больше, чем ЭДС одного источника:

Внутреннее сопротивление такой батареи будет также в N раз больше:

Рис. 152. Схема последовательного соединения источников тока

Для последовательного соединения источников тока закон Ома для полной цепи будет записываться:

Последовательное соединение источников τoιca удобно в том случае, когда сопротивление потребителя значительно больше внутреннего сопротивления одного источника тока.
Параллельным является соединение, при котором все одноименные полюса соединяется в один узел (рис. 1.53).

Pиc. 153. Схема параллельного соединения источников тока

Параллельное соединение применяют тогда, когда в цепи необходимо получить большое значение силы тока при небольшом напряжении.

Электродвижущая сила батареи параллельно соединенных одинаковых источников равна ЭДС одного источника:

Формула закона Ома для параллельного соединения источников имеет вид:

Параллельное соединения удобно тогда» когда сопротивление внешней части цепи значительно меньше внутреннего сопротивления одного источника.

При смешанном соединении батареи источников тока (параллельно или последовательно) в свою очередь соединяют последовательно или параллельно (рис. 1.54).

Pиc. 1.54. Смешанное соединение источников тoκa

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
• Сила и закон Ампера
• Закон взаимодействия прямолинейных параллельных проводников с током
• Сила Лоренца
• Звуковые волны в физике
• Электрическое поле в физике
• Работа по перемещению заряда в электростатическом поле
• Закон Ома для однородного участка электрической цепи